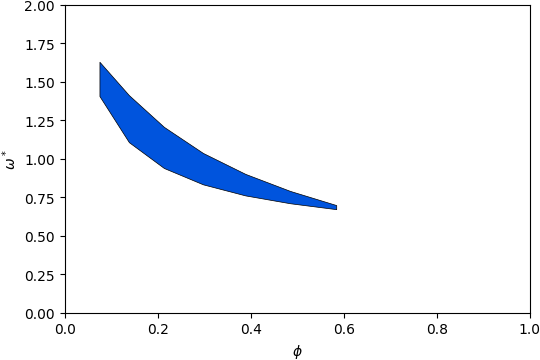
oP12-CuAsS (Inverse)

oP12–CuAsS (Inverse)

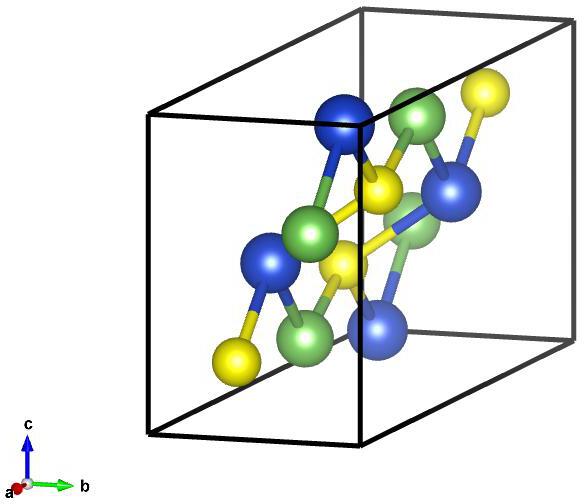
Image of oP12–CuAsS (Inverse), generated by Vesta

Lattice Vectors:

\[\begin{split}a_1 &= ~\hat{x}\\ a_2 &= 0.3307746463~\hat{y}\\ a_3 &= 0.4805675518~\hat{z}\\\end{split}\]

Space Group: 62

Point Group of Structure: \(mmm\)

Structure DOI: https://doi.org/10.1107/S1600536808004492

Source: Crystallographic Open Database #2217766

MPB Epsilon Input File: Download

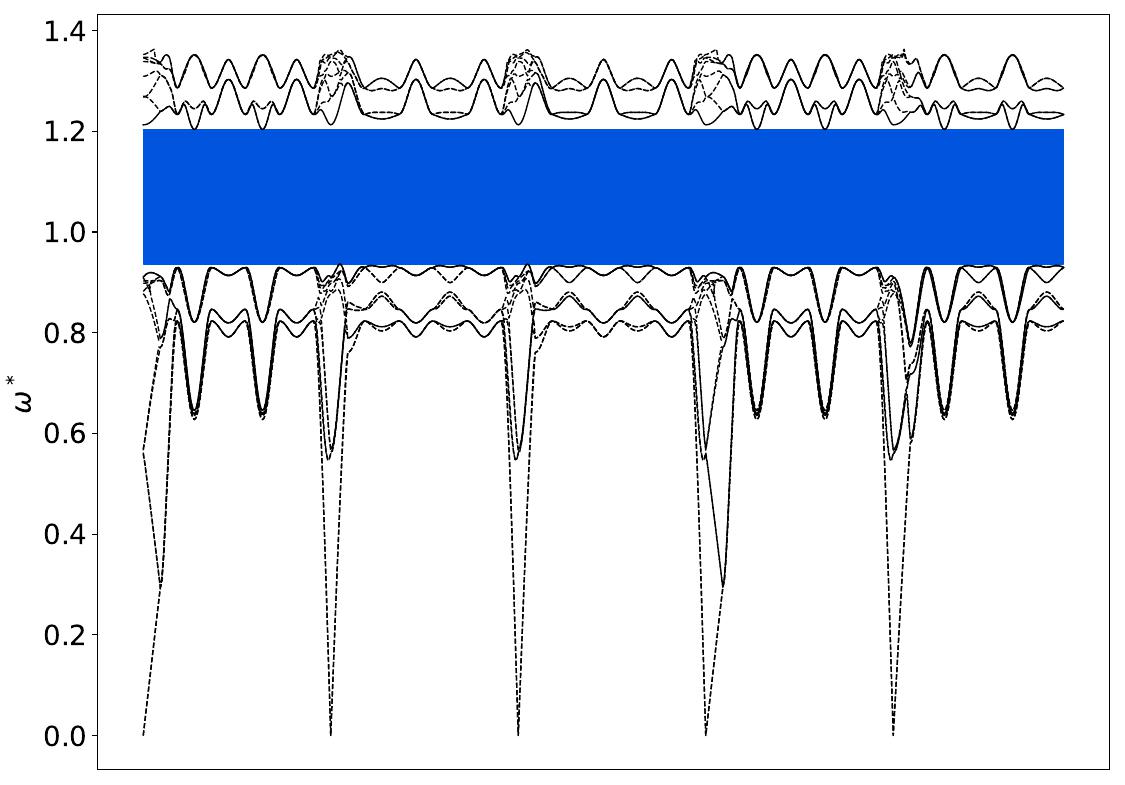
Gap Atlas for \(\varepsilon = 16\)

Gap Atlas for \(\varepsilon\) = 16 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 14\)

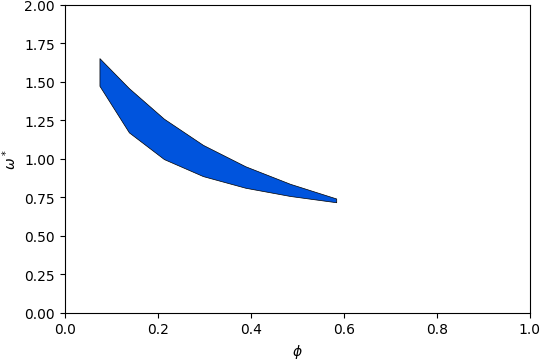
Gap Atlas for \(\varepsilon\) = 14 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 12\)

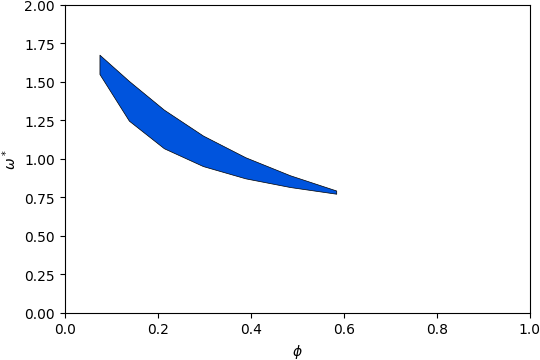
Gap Atlas for \(\varepsilon\) = 12 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 10\)

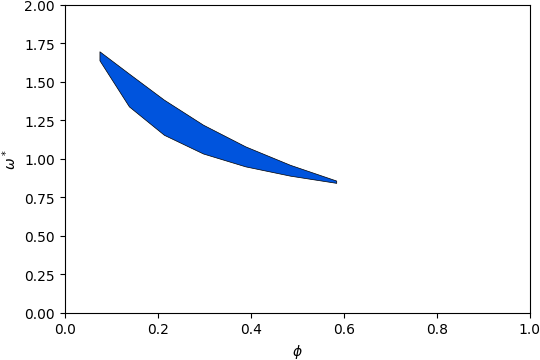
Gap Atlas for \(\varepsilon\) = 10 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 8\)

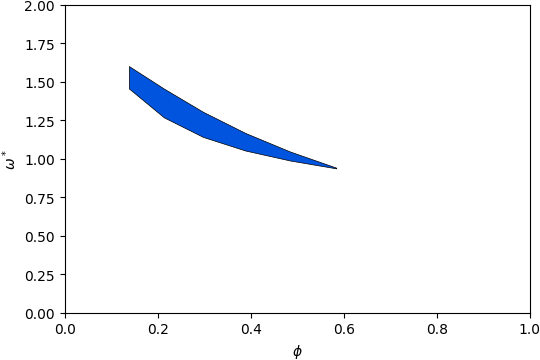
Gap Atlas for \(\varepsilon\) = 8 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 6\)

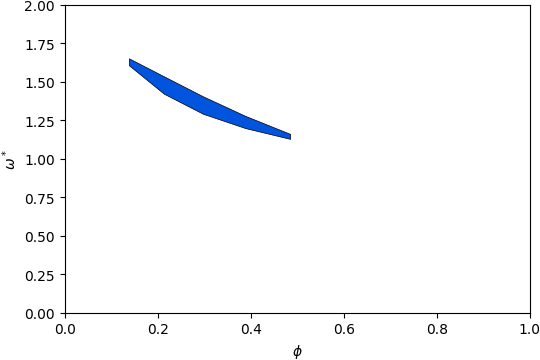
Gap Atlas for \(\varepsilon\) = 6 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 4\)

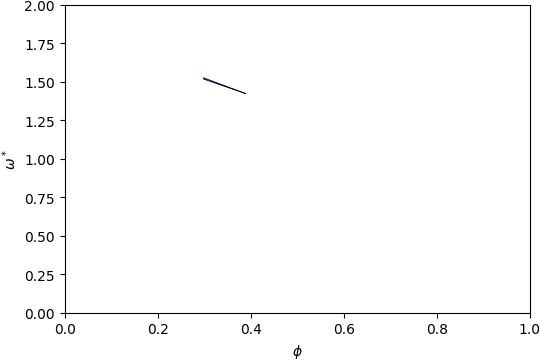
Gap Atlas for \(\varepsilon\) = 4 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 2\)

Gap Atlas for \(\varepsilon\) = 2 across filling fraction \(\phi\) and frequency \(\omega\).

Gap between Bands 12-13

Below is the band structure and isosurface of oP12–CuAsS (Inverse) at dielectric contrast \(\varepsilon = 16\), radius \(r = 0.15\) and filling fraction \(\phi = 0.215\).

Band Structure across first Brillouin Zone.

View along \(a_1\).