cF64-FeF3 (Inverse)

cF64–FeF₃ (Inverse)

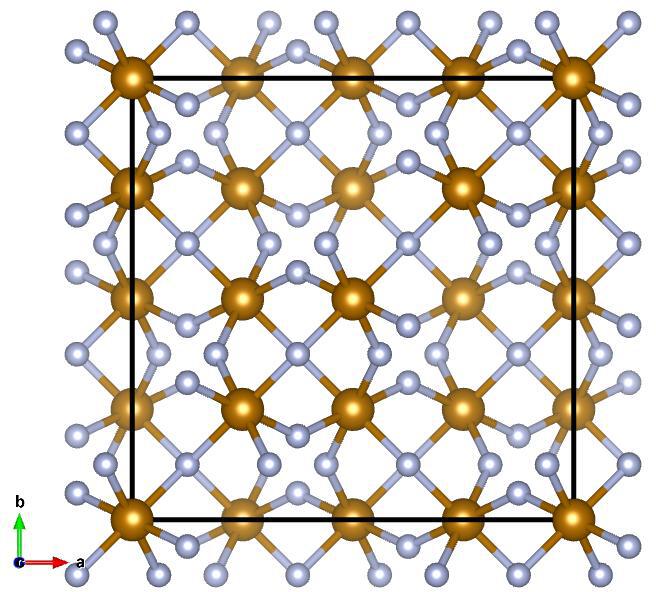
Image of cF64–FeF₃ (Inverse), generated by Vesta

Lattice Vectors:

\[\begin{split}a_1 &= 1/\sqrt{2}~\hat{y} + 1/\sqrt{2}~\hat{z}\\ a_2 &= 1/\sqrt{2}~\hat{x} + 1/\sqrt{2}~\hat{z}\\ a_3 &= 1/\sqrt{2}~\hat{x} + 1/\sqrt{2}~\hat{y}\\\end{split}\]

Space Group: 227

Point Group of Structure: \(m\bar{3}m\)

Structure DOI: https://doi.org/10.1016/0025-5408(86)90134-0

Photonics DOI: Gap(s) for space group 227 above band(s) 2 theorized in: https://doi.org/10.1038/nmat979,

Gap(s) above band(s) 8, 18 not previously studied

Source: Crystallographic Open Database #1000228

MPB Epsilon Input File: Download

Gap Atlas for \(\varepsilon = 16\)

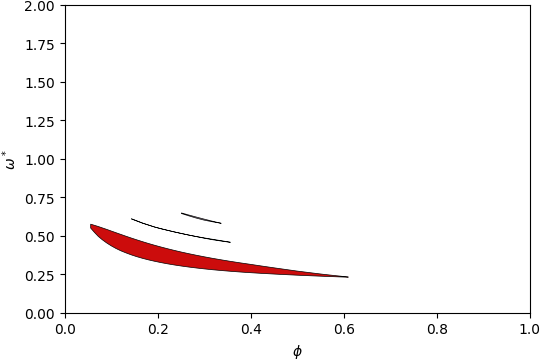
Gap Atlas for \(\varepsilon\) = 16 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 14\)

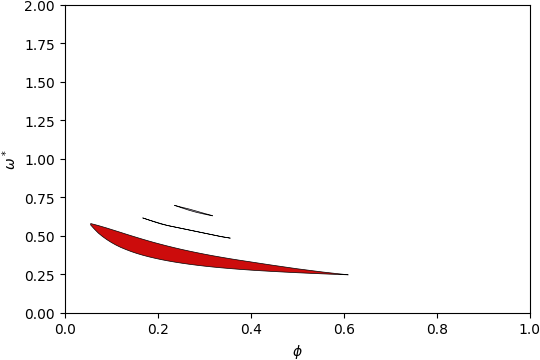
Gap Atlas for \(\varepsilon\) = 14 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 12\)

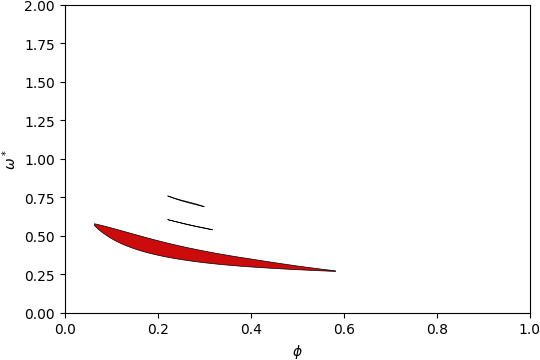
Gap Atlas for \(\varepsilon\) = 12 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 10\)

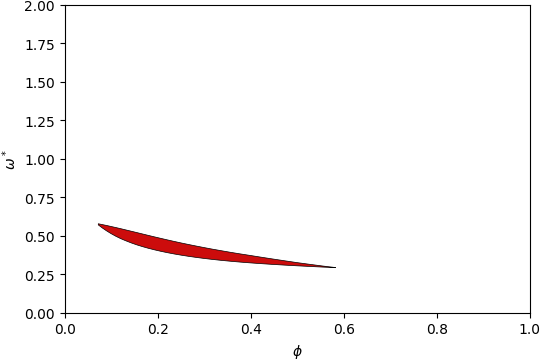
Gap Atlas for \(\varepsilon\) = 10 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 8\)

Gap Atlas for \(\varepsilon\) = 8 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 6\)

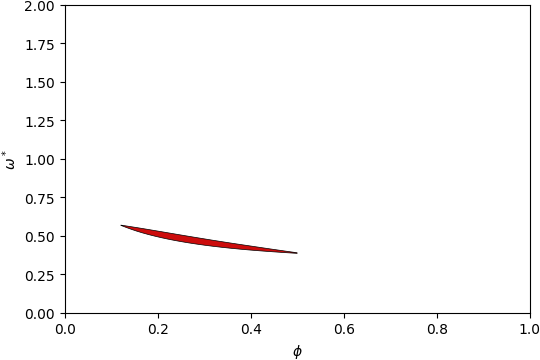
Gap Atlas for \(\varepsilon\) = 6 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 4\)

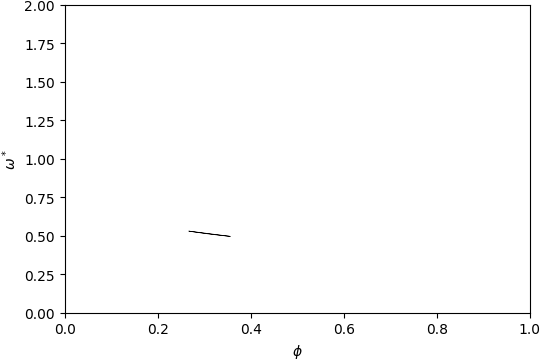
Gap Atlas for \(\varepsilon\) = 4 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 2\)

Gap Atlas for \(\varepsilon\) = 2 across filling fraction \(\phi\) and frequency \(\omega\).

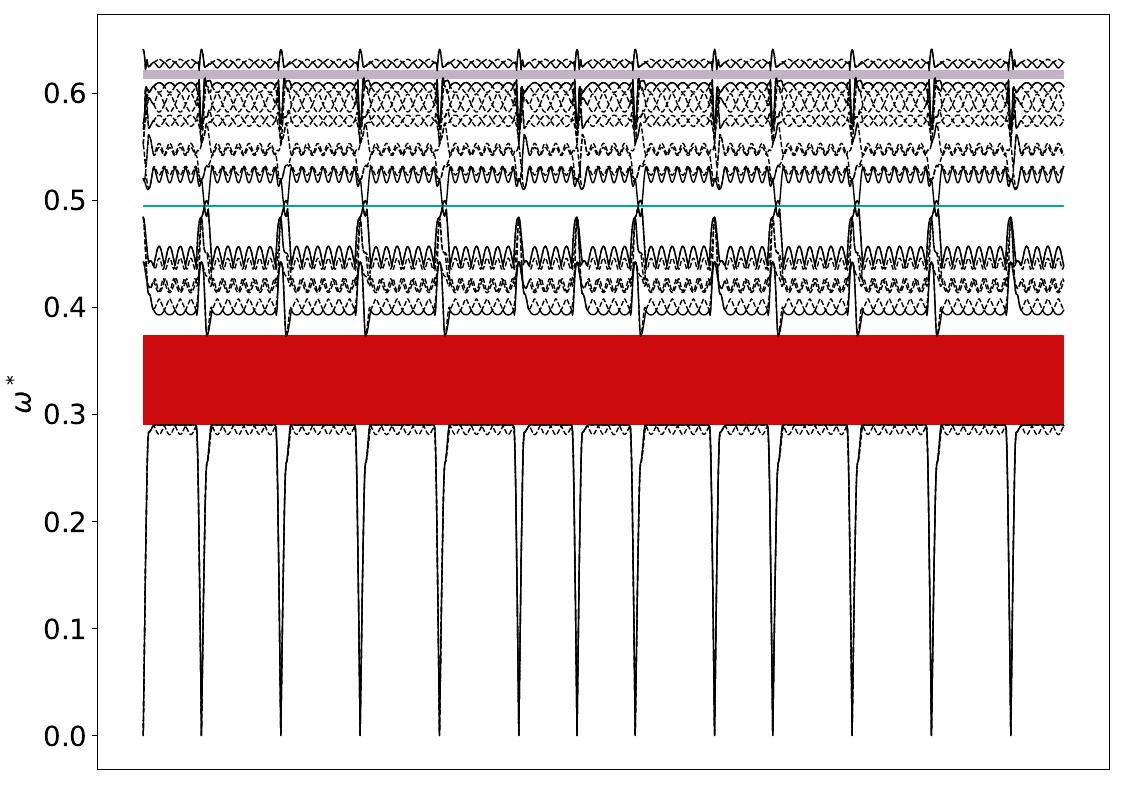
Gap between Bands 2-3

Below is the band structure and isosurface of cF64–FeF₃ (Inverse) at dielectric contrast \(\varepsilon = 16\), radius \(r = 0.265\) and filling fraction \(\phi = 0.194\).

Band Structure across first Brillouin Zone.

View along \(a_1\).

Gap between Bands 8-9

Below is the band structure and isosurface of cF64–FeF₃ (Inverse) at dielectric contrast \(\varepsilon = 16\), radius \(r = 0.225\) and filling fraction \(\phi = 0.318\).

Band Structure across first Brillouin Zone.

View along \(a_1\).

Gap between Bands 18-19

Below is the band structure and isosurface of cF64–FeF₃ (Inverse) at dielectric contrast \(\varepsilon = 16\), radius \(r = 0.235\) and filling fraction \(\phi = 0.283\).

Band Structure across first Brillouin Zone.

View along \(a_1\).