tI12-HfV2 (Direct)

tI12–HfV₂ (Direct)

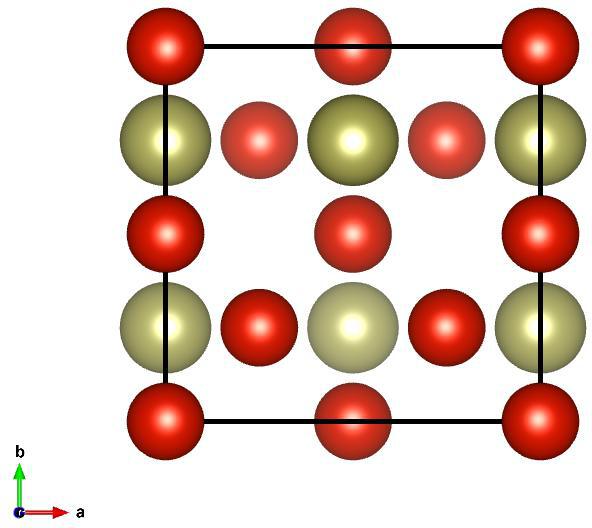
Image of tI12–HfV₂ (Direct), generated by Vesta

Lattice Vectors:

\[\begin{split}a_1 &= -0.4987313728~\hat{x} + 0.4987313728~\hat{y} + 0.7088963504~\hat{z}\\ a_2 &= 0.4987313728~\hat{x} - 0.4987313728~\hat{y} + 0.7088963504~\hat{z}\\ a_3 &= 0.4987313728~\hat{x} + 0.4987313728~\hat{y} - 0.7088963504~\hat{z}\\\end{split}\]

Space Group: 141

Point Group of Structure: \(4/mmm\)

Structure DOI: https://doi.org/10.1107/S0108768100003633

Photonics DOI: Gap(s) for space group 141 above band 2 theorized in: https://doi.org/10.1103/PhysRevLett.121.263903

Source: Crystallographic Open Database #2102112

MPB Epsilon Input File: Download

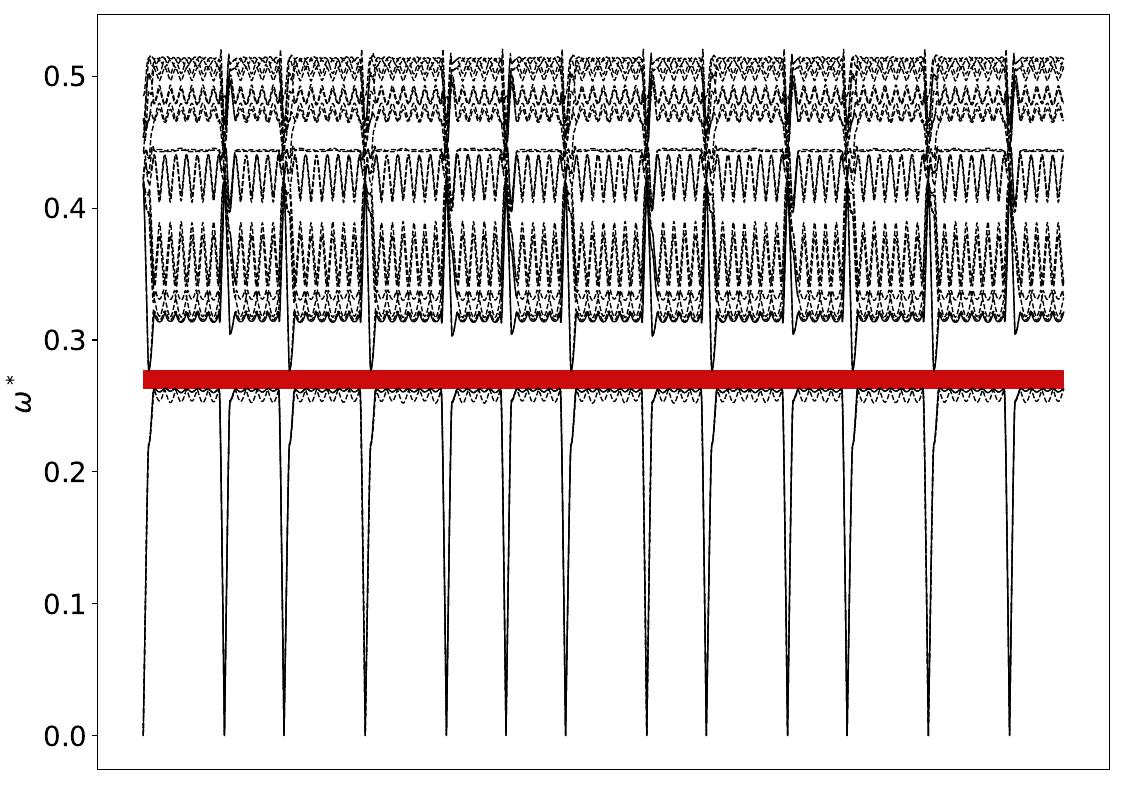
Gap Atlas for \(\varepsilon = 16\)

Gap Atlas for \(\varepsilon\) = 16 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 14\)

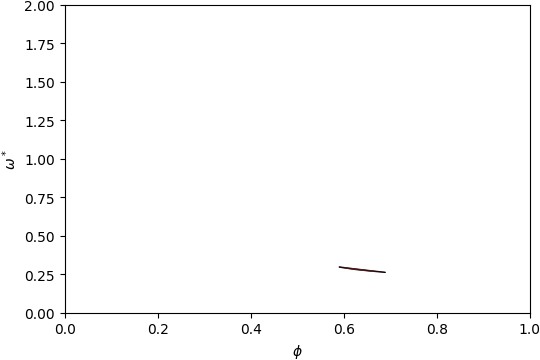
Gap Atlas for \(\varepsilon\) = 14 across filling fraction \(\phi\) and frequency \(\omega\).

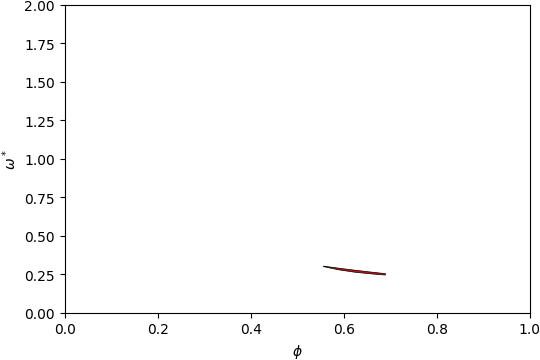
Gap Atlas for \(\varepsilon = 12\)

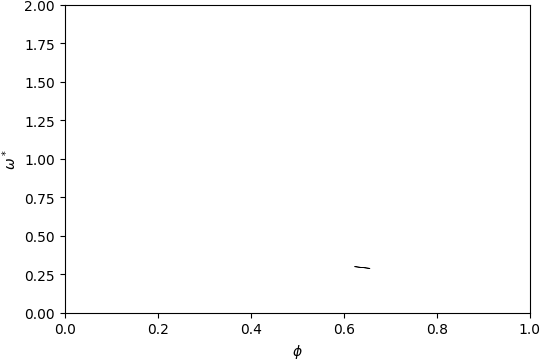
Gap Atlas for \(\varepsilon\) = 12 across filling fraction \(\phi\) and frequency \(\omega\).

Gap Atlas for \(\varepsilon = 10\)

Gap Atlas for \(\varepsilon\) = 10 across filling fraction \(\phi\) and frequency \(\omega\).

Gap between Bands 2-3

Below is the band structure and isosurface of tI12–HfV₂ (Direct) at dielectric contrast \(\varepsilon = 16\), radius \(r = 0.26\) and filling fraction \(\phi = 0.434\).

Band Structure across first Brillouin Zone.

View along \(a_1\).